Elemento supremo e ínfimo para niños
En matemáticas, el supremo y el ínfimo son conceptos importantes que nos ayudan a entender los límites de un grupo de números. Imagina que tienes una colección de números.
El supremo de un grupo de números es el número más pequeño que es igual o mayor que todos los números de ese grupo. Es como buscar el "techo" más bajo que cubre a todos los números. Se escribe como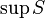 
.
De manera similar, el ínfimo de un grupo de números es el número más grande que es igual o menor que todos los números de ese grupo. Es como buscar el "piso" más alto que está por debajo de todos los números. Se escribe como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \inf S .
Contenido
¿Qué son las cotas superiores e inferiores?
Para entender el supremo y el ínfimo, primero necesitamos saber qué son las cotas.
Cota superior
Una cota superior de un grupo de números es cualquier número que es mayor o igual que todos los números de ese grupo. Por ejemplo, si tienes el grupo {1, 2, 3}, los números 3, 4, 5, 100 son todas cotas superiores.
El supremo es la cota superior más pequeña. Es decir, de todas las cotas superiores posibles, el supremo es la que está más cerca de los números del grupo.
Cota inferior
Una cota inferior de un grupo de números es cualquier número que es menor o igual que todos los números de ese grupo. Por ejemplo, si tienes el grupo {1, 2, 3}, los números 1, 0, -5, -100 son todas cotas inferiores.
El ínfimo es la cota inferior más grande. Es decir, de todas las cotas inferiores posibles, el ínfimo es la que está más cerca de los números del grupo.
Características importantes
- En el mundo de los números reales, si un grupo de números no está vacío y tiene un "techo" (está acotado superiormente), siempre tendrá un supremo. Lo mismo ocurre con el ínfimo si tiene un "piso" (está acotado inferiormente).
- Si un supremo o un ínfimo existen, ¡siempre son únicos! No puede haber dos supremos diferentes para el mismo grupo de números.
- Si tienes dos grupos de números, A y B, y los unes, el supremo del grupo unido será el más grande de los supremos de A y B. Lo mismo ocurre con el ínfimo, pero será el más pequeño.
* 
* 
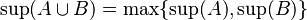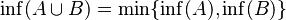
- Un grupo de números tiene un elemento máximo (el número más grande dentro del grupo) si y solo si su supremo es uno de los números de ese grupo. De manera similar, tiene un elemento mínimo si y solo si su ínfimo es uno de los números de ese grupo.
Ejemplos para entender mejor
Aquí tienes algunos ejemplos para ver cómo funcionan el supremo y el ínfimo:
- Para el grupo de números {1, 2, 3}:
* El supremo es 3. (Es la cota superior más pequeña y, en este caso, también es el número más grande del grupo). * El ínfimo es 1. (Es la cota inferior más grande y, en este caso, también es el número más pequeño del grupo).
- Para el grupo de números entre 0 y 1, sin incluir el 0 ni el 1 (por ejemplo, 0.1, 0.5, 0.999...):
* Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sup \{ x \in \mathbb{R} | 0 < x < 1 \} = 1 . El supremo es 1, aunque el 1 no esté en el grupo. * Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \inf \{ x \in \mathbb{R} | 0 < x < 1 \} = 0 . El ínfimo es 0, aunque el 0 no esté en el grupo.
- Para el grupo de números entre 0 y 1, incluyendo el 0 y el 1 (por ejemplo, 0, 0.1, 0.5, 0.999..., 1):
* Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sup \{ x \in \mathbb{R} | 0 \leq x \leq 1 \} = 1 . El supremo es 1, y en este caso, el 1 sí está en el grupo. * Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \inf \{ x \in \mathbb{R} | 0 \leq x \leq 1 \} = 0 . El ínfimo es 0, y en este caso, el 0 sí está en el grupo.
- Para el grupo de números positivos cuya raíz cuadrada es menor que 2 (por ejemplo, 1, 1.4, 1.41, etc.):
* Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sup \{ x \in \mathbb{Q^{+}} | x^2 \leq 2 \} = \sqrt{2} (la raíz cuadrada de 2).
- Para el grupo de números que se forman como 1 dividido por un número natural (1/1, 1/2, 1/3, 1/4, ...):
* Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \inf \left\{ \frac{1}{n} | n \in \mathbb{N} \right\} = 0 . A medida que 'n' se hace más grande, 1/n se acerca más y más a 0, pero nunca llega a ser 0. Por eso, 0 es el ínfimo.
Galería de imágenes
-
Un conjunto A de números reales (representados por círculos azules), un conjunto de cotas superiores de A (círculos rojos), y el mínimo de las cotas superiores, el supremo de A (diamante rojo).
