Ventana (función) para niños
Las ventanas son como "filtros" especiales que se usan en el mundo de las señales y el procesamiento de señales. Imagina que tienes una canción muy larga y solo quieres analizar un pedacito de ella. Las ventanas te ayudan a tomar ese pedacito sin que el inicio y el final suenen raros o cortados de golpe.
Cuando analizamos una señal, como una grabación de sonido o datos de un sensor, a menudo solo podemos ver una parte limitada de ella. Para hacer esto, multiplicamos la señal por una función ventana.
La ventana más sencilla es la rectangular. Piensa en ella como un interruptor: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): h(t) = \begin{cases} 1 & \mbox{ si } t \in [0,T] \\ 0 & \mbox{ resto.} \end{cases} Esto significa que la ventana deja pasar la señal (multiplicando por 1) solo durante un tiempo específico (de 0 a T) y la bloquea (multiplicando por 0) en cualquier otro momento. Así, solo vemos ese pedazo de la señal.
Al usar una ventana, cambiamos cómo se ve la señal cuando la analizamos en el "dominio de la frecuencia" (que nos dice qué tan agudos o graves son los sonidos, por ejemplo). Existen diferentes tipos de ventanas, y cada una ayuda a obtener resultados distintos en este análisis.
Aplicaciones de las Ventanas
Las funciones de ventana se usan en muchas áreas, como:
- Analizar y modificar el sonido.
- Diseñar filtros para señales.
- Mejorar la forma en que funcionan las antenas.
Análisis de Espectro
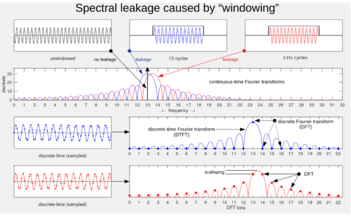
Imagina que quieres saber qué frecuencias (como las notas musicales) tiene una señal. La Transformada de Fourier es una herramienta matemática que nos ayuda con esto. Sin embargo, si solo analizamos un pedazo de la señal, la Transformada de Fourier puede mostrar "frecuencias fantasma" que no están realmente ahí. Esto se llama manchado espectral o "goteo".
Para evitar este problema, multiplicamos la señal por una función de ventana antes de aplicar la Transformada de Fourier. La ventana ayuda a que el análisis sea más preciso.
¿Cómo Elegir la Mejor Ventana?
Cuando analizamos una señal, el uso de una ventana puede hacer que aparezcan esas "frecuencias fantasma" (manchado espectral). Este manchado es más fuerte cerca de la frecuencia real y se debilita a medida que nos alejamos.
Si una señal tiene dos frecuencias muy diferentes, el manchado de una puede ocultar a la otra, especialmente si una es mucho más débil. Esto se llama un problema de alto rango dinámico. Si las dos frecuencias son muy parecidas, el problema es de alta resolución.
No hay una ventana perfecta para todo. Debemos elegir la ventana adecuada según lo que queramos analizar. Algunas ventanas, como las de Hann o Hamming, son buenas para casos intermedios.
Señales Digitales
Cuando trabajamos con señales que han sido "muestreadas" (convertidas en números, como en un archivo de audio digital), usamos una transformada de Fourier discreta (DFT). La DFT nos da una "foto" de las frecuencias de la señal.
La Figura 2 muestra cómo una ventana rectangular afecta la señal. La frecuencia real de la señal está en el punto "13". Todo lo demás es "goteo" o manchado. La Figura 3 compara cómo diferentes ventanas afectan este manchado.
Ruido y Ancho de Banda
El manchado espectral también está relacionado con el "ancho de banda de ruido". Cuanto más manchado hay, mayor es este ancho de banda. Esto es importante porque afecta la cantidad de ruido que vemos en el análisis de la señal.
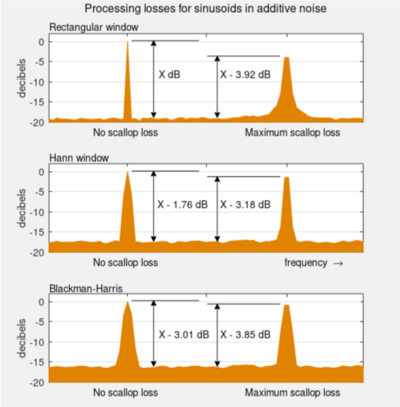
Ganancia de Procesamiento
En el procesamiento de señales, buscamos mejorar la calidad de una señal, por ejemplo, separando la señal que nos interesa del ruido. Si tenemos una señal con ruido, el análisis espectral puede ayudar a concentrar la energía de la señal en una frecuencia, mientras que el ruido se distribuye. Esto mejora la relación señal/ruido (S/R), lo que significa que la señal se escucha más clara que el ruido. A esto se le llama "ganancia de procesamiento".
Tipos Comunes de Ventanas
Aquí te mostramos algunas de las ventanas más usadas, con sus fórmulas matemáticas. La letra 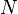 representa el tamaño de la ventana.
representa el tamaño de la ventana.
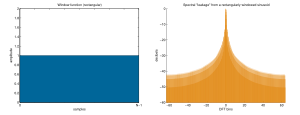
Rectangular
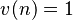 Esta es la ventana más simple, que simplemente "corta" un pedazo de la señal.
Esta es la ventana más simple, que simplemente "corta" un pedazo de la señal.
Hann
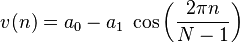
 A menudo se le llama "Hanning" por error, pero su nombre correcto es Hann, en honor a Julius von Hann. También se le conoce como "coseno elevado".
A menudo se le llama "Hanning" por error, pero su nombre correcto es Hann, en honor a Julius von Hann. También se le conoce como "coseno elevado".
Hamming
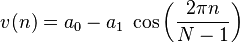
 Nombrada en honor a Richard Hamming.
Nombrada en honor a Richard Hamming.
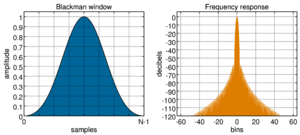
Blackman
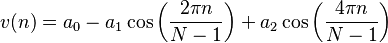

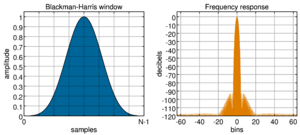
Blackman-Harris
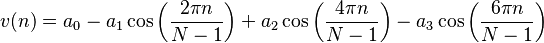

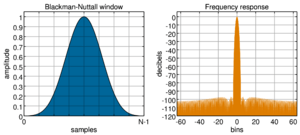
Blackman-Nuttall
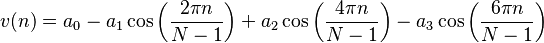

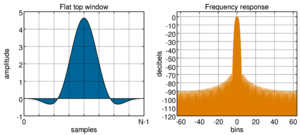
Flat top
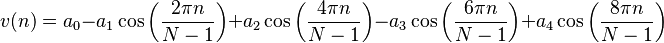
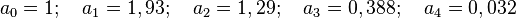
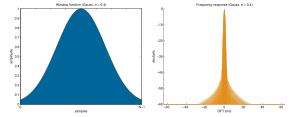
Gauss
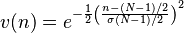
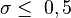
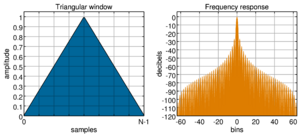
Triangular
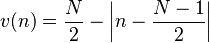
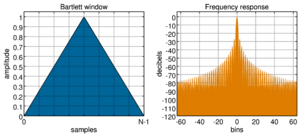
Bartlett
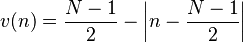
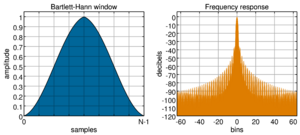
Bartlett-Hann
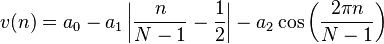
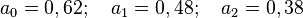
Kaiser
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): w_k = \left\{ \begin{matrix} \frac{I_0(\pi\alpha \sqrt{1 - (2k/n-1)^2})} {I_0(\pi\alpha)} & \mbox{si } 0 \leq k \leq n \\ \\ 0 & \mbox{resto} \\ \end{matrix} \right. Donde I0 es una función matemática especial llamada función de Bessel modificada, y α es un número que cambia la forma de la ventana.
Galería de imágenes
Véase también
 En inglés: Window function Facts for Kids
En inglés: Window function Facts for Kids