Proporcionalidad para niños
La proporcionalidad es una forma de comparar dos o más cantidades que cambian juntas de manera constante. Imagina que si una cantidad aumenta, la otra también lo hace de forma predecible, o si una disminuye, la otra también lo hace de la misma manera. Es una relación fija entre ellas.
Contenido
Símbolo de Proporcionalidad
El símbolo matemático '∝' se usa para mostrar que dos valores son proporcionales. Por ejemplo, si escribimos A ∝ B, significa que A es proporcional a B.
Proporcionalidad Directa
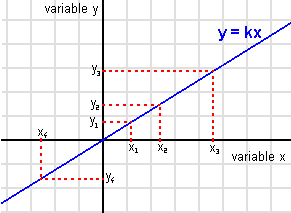
Cuando dos cantidades, digamos X e Y, son directamente proporcionales, significa que si una aumenta, la otra también aumenta en la misma proporción. Y si una disminuye, la otra disminuye de la misma manera.
Esto se puede escribir con una fórmula: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y = kx
Aquí, 'k' es un número fijo que llamamos la constante de proporcionalidad. Este número nos dice cuánto cambia Y por cada cambio en X.
Por ejemplo, si el peso de una muestra de hierro es directamente proporcional a su volumen, significa que si tienes el doble de volumen de hierro, tendrás el doble de peso. La relación entre el peso y el volumen siempre será la misma, y esa relación es la constante de proporcionalidad.
Ejemplo de Receta
Imagina que tienes una receta de pastel para cuatro personas que necesita 200 gramos de harina. Si quieres hacer el pastel para cinco personas, ¿cuánta harina necesitarías?
Aquí, la cantidad de harina es directamente proporcional al número de personas. Para saber cuánto necesita cada persona, divides 200 g entre 4 personas, lo que da 50 g por persona. Luego, multiplicas 50 g por las 5 personas, y obtienes 250 g de harina.
También puedes calcular un factor de cambio: 5 personas / 4 personas = 1.25. Entonces, multiplicas la cantidad original de harina por 1.25: 200 g * 1.25 = 250 g.
Esta situación se puede ver en una tabla de proporcionalidad. La constante 'k' en este caso es 5/4 o 1.25.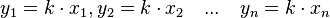 
Cuando representamos gráficamente la proporcionalidad directa, siempre obtenemos una línea recta que empieza en el punto (0,0) de un sistema de coordenadas. Esto significa que si no hay personas, no hay harina, lo cual tiene sentido.
Propiedades de la Proporcionalidad Directa
La relación de proporcionalidad directa tiene algunas propiedades interesantes:
- Reflexiva: Cualquier cantidad es proporcional a sí misma (con una constante de 1).
- Simétrica: Si Y es proporcional a X, entonces X también es proporcional a Y (con la constante inversa).
- Transitiva: Si X es proporcional a Y, e Y es proporcional a Z, entonces X es proporcional a Z.
Estas propiedades hacen que la proporcionalidad sea una "relación de equivalencia", lo que significa que las cantidades proporcionales se comportan de manera similar entre sí.
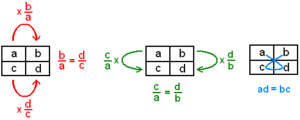
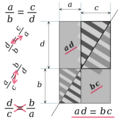
Una proporción es cuando dos razones son iguales. Por ejemplo, si a : b = c : d, se lee "a es a b como c es a d". En una proporción, los números de los extremos (a y d) y los números del medio (b y c) tienen una relación especial: el producto de los extremos es igual al producto de los medios (a * d = b * c).
Ejemplo de Albañiles
Dos albañiles construyeron una pared de 12 metros cuadrados en tres horas. ¿Qué superficie construirán cinco albañiles en cuatro horas?
Aquí, el trabajo depende de dos cosas: el número de albañiles y el tiempo.
- Suponemos que todos los albañiles trabajan igual de rápido.
- Suponemos que no se cansan y su rendimiento no cambia con el tiempo.
Primero, calculamos cuánto harían dos albañiles en cuatro horas. Como el número de albañiles es el mismo, solo cambia el tiempo. Si en 3 horas hacen 12 m², en 4 horas harán más. Multiplicamos 12 m² por (4/3). 12 * (4/3) = 16 m².
Ahora, sabemos que dos albañiles hacen 16 m² en cuatro horas. ¿Cuánto harán cinco albañiles en cuatro horas? El tiempo es el mismo, pero el número de albañiles cambia. Multiplicamos 16 m² por (5/2). 16 * (5/2) = 40 m².
Así, cinco albañiles construirán 40 metros cuadrados en cuatro horas.
Proporcionalidad Inversa
La proporcionalidad inversa es lo contrario de la directa. Si una cantidad aumenta, la otra disminuye, pero su producto se mantiene constante.
Formalmente, si Y es inversamente proporcional a X, significa que existe una constante 'k' (que no es cero) tal que: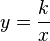 
Ejemplo de Viaje en Auto
Dos autos recorren el mismo camino. El primer auto tardó 2.5 horas yendo a 70 km/h. El segundo auto va a 100 km/h. ¿Cuánto tiempo tardará el segundo auto?
Aquí, cuanto mayor sea la velocidad, menor será el tiempo de viaje. Esto es una proporcionalidad inversa. Si multiplicas la velocidad por dos, el tiempo se dividirá por dos.
Podemos usar la idea de que el producto de la velocidad y el tiempo es constante (es la distancia total). Para el primer auto: 70 km/h * 2.5 h = 175 km. Para el segundo auto, la distancia es la misma (175 km). Si va a 100 km/h, el tiempo será: Tiempo = Distancia / Velocidad = 175 km / 100 km/h = 1.75 horas. 1.75 horas es 1 hora y 45 minutos.
El gráfico de dos variables inversamente proporcionales en un plano de coordenadas es una curva llamada hipérbola.
Aplicación en Geometría
El concepto de proporcionalidad es muy importante en geometría, especialmente cuando hablamos de triángulos semejantes. Dos triángulos son semejantes si tienen la misma forma, aunque sean de diferente tamaño. Sus lados correspondientes son proporcionales. Por ejemplo, si un triángulo es el doble de grande que otro, todos sus lados serán el doble de largos.
Repartos Proporcionales
Los repartos proporcionales consisten en dividir una cantidad en partes que son proporcionales a otros números.
Reparto Directamente Proporcional
Imagina que quieres repartir 120 dulces entre tres amigos en partes directamente proporcionales a los números 2, 3 y 5. Esto significa que el amigo que tiene el número 5 recibirá más dulces que el que tiene el 2.
Para resolverlo: 1. Suma los números de las proporciones: 2 + 3 + 5 = 10. 2. Divide la cantidad total (120 dulces) entre esa suma: 120 / 10 = 12. Este es el valor de cada "parte". 3. Multiplica este valor por cada número de la proporción: * Amigo 1 (proporción 2): 2 * 12 = 24 dulces. * Amigo 2 (proporción 3): 3 * 12 = 36 dulces. * Amigo 3 (proporción 5): 5 * 12 = 60 dulces. Si sumas 24 + 36 + 60, obtendrás 120 dulces.
Reparto Inversamente Proporcional
Un padre quiere repartir 6200 acciones de una empresa entre sus tres hijos, de 4, 6 y 10 años, en partes inversamente proporcionales a sus edades. Esto significa que el hijo más joven recibirá más acciones y el mayor recibirá menos.
Para hacer un reparto inversamente proporcional, lo convertimos en un reparto directamente proporcional usando las inversas de las edades:
- Hijo de 4 años: 1/4
- Hijo de 6 años: 1/6
- Hijo de 10 años: 1/10
Para trabajar con estas fracciones, buscamos un denominador común, que es 60.
- 1/4 = 15/60
- 1/6 = 10/60
- 1/10 = 6/60
Ahora, repartimos las 6200 acciones directamente proporcionales a 15, 10 y 6. 1. Suma las nuevas proporciones: 15 + 10 + 6 = 31. 2. Divide el total de acciones entre esa suma: 6200 / 31 = 200. 3. Multiplica este valor por cada nueva proporción: * Hijo de 4 años (proporción 15): 15 * 200 = 3000 acciones. * Hijo de 6 años (proporción 10): 10 * 200 = 2000 acciones. * Hijo de 10 años (proporción 6): 6 * 200 = 1200 acciones. Si sumas 3000 + 2000 + 1200, obtendrás 6200 acciones.
Galería de imágenes
-
Los dos rectángulos con franjas son semejantes, los cocientes de sus dimensiones se indican horizontalmente en la imagen. La duplicación de la escala del triángulo con franjas se indica oblicuamente en la imagen.
-
Tres tablas de proporcionalidad 2x2.
Véase también
En inglés: Proportionality (mathematics) Facts for Kids
