Quicksort para niños
El ordenamiento rápido (conocido como quicksort en inglés) es un método muy eficiente para organizar listas de elementos, como números o palabras, de menor a mayor o de mayor a menor. Fue creado por un científico de la computación británico llamado C. A. R. Hoare.
Contenido
¿Qué es el Ordenamiento Rápido (Quicksort)?
El Quicksort es un tipo de algoritmo de ordenamiento. Imagina que tienes una pila de cartas desordenadas y quieres organizarlas. El Quicksort es como una estrategia inteligente para hacer esto de forma rápida. Es uno de los algoritmos más usados en la computación por su velocidad.
¿Cómo funciona el algoritmo Quicksort?
El Quicksort funciona dividiendo una lista grande en partes más pequeñas y ordenándolas por separado. Luego, junta esas partes ya ordenadas para formar la lista completa.
El papel del "pivote"
El primer paso es elegir un elemento especial de la lista, al que llamamos pivote. Este pivote es como un punto de referencia.
Pasos clave del Quicksort
- Elegir un pivote: Se selecciona un elemento de la lista para que sea el pivote.
- Reorganizar la lista: Todos los elementos que son más pequeños que el pivote se mueven a un lado de él, y todos los que son más grandes se mueven al otro lado. Los elementos que son iguales al pivote pueden ir a cualquier lado. Después de este paso, el pivote ya está en su lugar correcto dentro de la lista final ordenada.
- Dividir la lista: La lista se divide en dos partes: una con los elementos menores que el pivote y otra con los elementos mayores.
- Repetir el proceso: Estos mismos pasos se repiten una y otra vez (de forma recursiva) en cada una de las dos nuevas sublistas, hasta que todas las sublistas tengan solo un elemento o estén ya ordenadas. Cuando este proceso termina, ¡toda la lista original estará ordenada!
¿Qué tan rápido es Quicksort?
La velocidad del Quicksort depende mucho de cómo se elige el pivote.
- El mejor escenario: Si el pivote divide la lista justo por la mitad, el algoritmo es muy rápido. Su velocidad se describe como O(n·log n), lo que significa que es muy eficiente incluso con listas grandes.
- El peor escenario: Si el pivote siempre termina en un extremo de la lista (por ejemplo, si la lista ya está casi ordenada y siempre se elige el primer elemento como pivote), el algoritmo puede ser más lento. En este caso, su velocidad es O(n²).
- El caso más común: En promedio, el Quicksort es muy eficiente, con una velocidad de O(n·log n).
Por eso, muchas mejoras al Quicksort se enfocan en cómo elegir el mejor pivote.
Elegir el mejor "pivote"
Hay varias formas de elegir el pivote para que el Quicksort sea más eficiente:
- Elegir cualquier elemento: Es la forma más sencilla, pero a veces puede llevar al peor escenario.
- Buscar el elemento central: Se puede recorrer la lista para encontrar el elemento que estaría justo en el medio si la lista estuviera ordenada. Esto asegura que el algoritmo sea siempre rápido, pero el cálculo inicial puede tardar un poco.
- Tomar tres elementos: Una opción intermedia es elegir tres elementos (por ejemplo, el primero, el del medio y el último) y usar el valor que esté en el medio de esos tres como pivote.
Cómo se mueven los elementos
Para mover los elementos alrededor del pivote de forma eficiente, se usan dos "marcadores" o índices: uno que avanza desde el principio de la lista (llamado i) y otro que retrocede desde el final (llamado j).
- El marcador i avanza si el elemento que encuentra es menor que el pivote.
- El marcador j retrocede si el elemento que encuentra es mayor que el pivote.
- Cuando i encuentra un elemento mayor que el pivote y j encuentra uno menor, ¡se intercambian!
- Este proceso se repite hasta que los marcadores i y j se cruzan. En ese punto, el pivote se coloca donde se cruzaron, y ya sabemos que todos los elementos a su izquierda son menores y a su derecha son mayores.
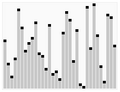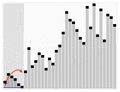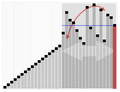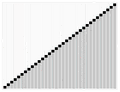
Un ejemplo de Quicksort paso a paso
Vamos a ordenar la lista de números: 5 - 3 - 7 - 6 - 2 - 1 - 4. Elegiremos el último elemento, el 4, como nuestro pivote (p). Los marcadores son i y j.
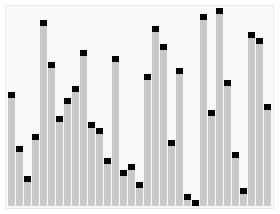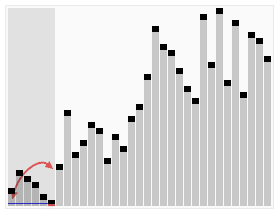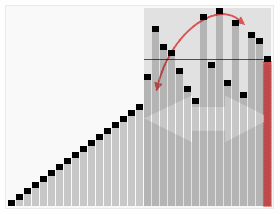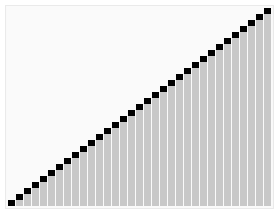
1. Lista inicial. El pivote es 4.
5 - 3 - 7 - 6 - 2 - 1 - 4
p
2. Comparamos 5 (en 'i') y 1 (en 'j') con el pivote 4.
5 - 3 - 7 - 6 - 2 - 1 - 4
i j p
3. Como 5 es mayor que 4 y 1 es menor que 4, los intercambiamos.
1 - 3 - 7 - 6 - 2 - 5 - 4
i j p
4. Avanzamos 'i' y 'j'.
1 - 3 - 7 - 6 - 2 - 5 - 4
i j p
5. 3 es menor que 4: 'i' avanza. 2 es menor que 4: 'j' se queda.
1 - 3 - 7 - 6 - 2 - 5 - 4
i j p
6. 7 es mayor que 4 y 2 es menor que 4: los intercambiamos.
1 - 3 - 2 - 6 - 7 - 5 - 4
i j p
7. Avanzamos 'i' y 'j'. ¡Se cruzan!
1 - 3 - 2 - 6 - 7 - 5 - 4
iyj p
8. Los marcadores se cruzaron. Ahora, intercambiamos el elemento en la posición 'i' (que es 6) con el pivote (4).
1 - 3 - 2 - 4 - 7 - 5 - 6
p
Ahora el 4 está en su lugar final. La lista se divide en dos: (1 - 3 - 2) y (7 - 5 - 6). 9. Aplicamos el mismo proceso a la sublista de la izquierda: (1 - 3 - 2). El pivote será 2.
1 - 3 - 2
Después de los pasos, esta sublista se ordena a (1 - 2 - 3). 10. El mismo procedimiento se aplica a la otra sublista (7 - 5 - 6). Se ordenará a (5 - 6 - 7). 11. Al finalizar y unir todas las sublistas, la lista inicial queda ordenada:
1 - 2 - 3 - 4 - 5 - 6 - 7
¿Cuándo usar otro método de ordenamiento?
Aunque Quicksort es muy bueno, a veces puede ser lento si la elección del pivote no es la ideal, especialmente con listas que ya están casi ordenadas.
- Listas muy pequeñas: Para listas con muy pocos elementos (menos de 8-15), otros algoritmos más sencillos, como el algoritmo de inserción, pueden ser más rápidos.
- Casos especiales: Para evitar que Quicksort se vuelva lento en situaciones difíciles, existen versiones mejoradas como el algoritmo introsort. Este algoritmo combina Quicksort con otros métodos para asegurar que siempre sea eficiente.
Galería de imágenes
Véase también
 En inglés: Quicksort Facts for Kids
En inglés: Quicksort Facts for Kids
Enlaces externos