Métodos numéricos para ecuaciones diferenciales ordinarias para niños
Los métodos numéricos para ecuaciones diferenciales ordinarias son como herramientas especiales que usamos en matemáticas para encontrar soluciones aproximadas a problemas que describen cómo cambian las cosas. Imagina que tienes una ecuación que te dice cómo se mueve un cohete o cómo crece una población de animales. A veces, estas ecuaciones son tan complicadas que no podemos encontrar una respuesta exacta usando las matemáticas normales.
Ahí es donde entran los métodos numéricos. Nos permiten calcular una solución que es muy, muy cercana a la real, lo cual es suficiente para muchas aplicaciones prácticas, como en la ingeniería o la ciencia. Es como si no pudieras medir algo con una regla exacta, pero puedes usar una cinta métrica para obtener una medida muy buena.
Estas ecuaciones diferenciales aparecen en muchas áreas de la ciencia, como la física (para el movimiento), la química (para las reacciones), la biología (para el crecimiento de poblaciones) y la economía (para modelos financieros).
Contenido
¿Qué es un problema de valor inicial?
Para entender estos métodos, primero necesitamos saber qué es un "problema de valor inicial" (PVI). Piensa en una ecuación que describe cómo algo cambia, por ejemplo, la velocidad de un coche. Si solo sabes cómo cambia la velocidad, no sabes dónde está el coche al principio. Un PVI te da la ecuación de cambio y también te dice dónde empieza el coche (su "valor inicial").
Una ecuación diferencial de primer orden es un PVI que se ve así:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y'(t) = f(t,y(t)), \qquad y(t_0)=y_0
Aquí, 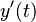 significa cómo cambia algo (su derivada), Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(t,y(t)) es una función que describe ese cambio, y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y(t_0)=y_0 es el punto de partida. "Primer orden" significa que solo aparece la primera derivada en la ecuación.
significa cómo cambia algo (su derivada), Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(t,y(t)) es una función que describe ese cambio, y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y(t_0)=y_0 es el punto de partida. "Primer orden" significa que solo aparece la primera derivada en la ecuación.
Podemos convertir ecuaciones más complejas (de orden superior) en un sistema de ecuaciones de primer orden. Por ejemplo, una ecuación que describe la aceleración de algo se puede convertir en dos ecuaciones de primer orden: una para la velocidad y otra para la posición.
Es importante saber que los problemas de valor inicial son diferentes de los "problemas de condición de frontera". En estos últimos, conoces el valor de la solución en varios puntos, no solo al principio. Para ellos se usan otros métodos.
Tipos de métodos numéricos
Los métodos numéricos para resolver problemas de valor inicial se dividen en dos grandes grupos: los métodos multipaso lineales y los métodos de Runge-Kutta. También se pueden clasificar en "explícitos" o "implícitos".
- Los métodos explícitos son más directos: calculan el siguiente paso usando solo la información que ya conocemos.
- Los métodos implícitos son un poco más complejos: para calcular el siguiente paso, necesitan resolver otra ecuación. Esto puede llevar más tiempo, pero a menudo son más estables para ciertos tipos de ecuaciones, permitiendo pasos más grandes.
El Método de Euler
El método de Euler es uno de los métodos numéricos más sencillos y fue descrito por Leonhard Euler en 1768. Es como si estuvieras caminando y, para saber dónde estarás en el siguiente paso, miras la dirección en la que vas ahora y das un pequeño paso en esa dirección.
Para usarlo, tomamos la ecuación diferencial y la aproximamos usando una "diferencia finita". Esto significa que en lugar de la derivada exacta, usamos una fórmula que nos dice cuánto cambia la función en un pequeño intervalo de tiempo.
La fórmula del método de Euler es:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y_{n+1} = y_n + hf(t_n,y_n).
Aquí, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y_n es nuestra estimación actual de la solución, 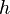 es el "tamaño del paso" (cuán grande es el salto que damos), y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(t_n,y_n) es la función que nos dice cómo cambia la solución en ese punto. Repetimos este cálculo una y otra vez para ir avanzando en el tiempo y encontrar la solución aproximada.
es el "tamaño del paso" (cuán grande es el salto que damos), y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(t_n,y_n) es la función que nos dice cómo cambia la solución en ese punto. Repetimos este cálculo una y otra vez para ir avanzando en el tiempo y encontrar la solución aproximada.
Este es un ejemplo de un método explícito, porque el nuevo valor Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y_{n+1} se calcula directamente a partir de los valores anteriores conocidos.
El Método de Euler hacia atrás
Existe una variación llamada "método de Euler hacia atrás". En lugar de usar la información del punto actual para predecir el futuro, usa la información del punto futuro (que aún no conocemos) para calcularlo.
La fórmula es:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y_{n+1} = y_n + hf(t_{n+1},y_{n+1}).
Como puedes ver, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y_{n+1} aparece en ambos lados de la ecuación. Esto lo convierte en un método implícito. Para encontrar Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y_{n+1} , necesitamos resolver una ecuación adicional, lo que puede ser más complicado. Sin embargo, estos métodos implícitos suelen ser más estables para resolver ecuaciones que son "rígidas" (que cambian muy rápidamente en algunas partes), permitiendo usar pasos de tiempo más grandes.
Generalizaciones y métodos avanzados
El método de Euler es simple, pero a menudo no es lo suficientemente preciso. Por eso, los matemáticos han desarrollado métodos de "orden superior" que dan resultados más exactos.
- Métodos multipaso: En lugar de usar solo el valor anterior (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y_n ) para calcular el siguiente (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y_{n+1} ), estos métodos usan varios valores anteriores. Un ejemplo es el "método del salto de rana".
- Métodos de Runge-Kutta: Estos métodos usan más puntos dentro del intervalo entre Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): t_n y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): t_{n+1} para obtener una mejor estimación. El método de Runge-Kutta de cuarto orden es muy popular por su buena precisión.
Además, las implementaciones modernas de estos métodos suelen incluir características avanzadas:
- Tamaño de paso variable: En lugar de usar siempre el mismo tamaño de paso, el método ajusta el tamaño del paso automáticamente para mantener el error por debajo de un cierto nivel. Esto hace que los cálculos sean más eficientes.
- Orden variable: Algunos métodos pueden cambiar dinámicamente entre diferentes órdenes de precisión para adaptarse mejor al problema.
- Salida densa: Permiten obtener aproximaciones de la solución en cualquier punto del intervalo, no solo en los puntos donde se calculó la solución.
Historia de los métodos numéricos
El desarrollo de estos métodos ha sido un viaje largo e interesante:
- 1768: Leonhard Euler publica su famoso método.
- 1824: Augustin Louis Cauchy demuestra que el método de Euler funciona bien (converge).
- 1855: Se menciona por primera vez el método multipaso lineal de John Couch Adams.
- 1895: Carl Runge publica el primer método de Runge-Kutta.
- 1901: Martin Wilhelm Kutta describe el popular método de Runge-Kutta de cuarto orden.
- 1952: Charles F. Curtiss y Joseph Oakland Hirschfelder usan por primera vez el término "ecuación rígida".
- 1963: Germund Dahlquist introduce el concepto de "A-estabilidad", que es importante para entender la estabilidad de los métodos.
Soluciones numéricas para problemas de valor límite
Los problemas de valor límite son un poco diferentes de los problemas de valor inicial. En lugar de conocer el punto de partida, conoces el valor de la solución en dos o más puntos diferentes (los "límites").
Para resolverlos numéricamente, a menudo se usa el "método de las diferencias finitas". Este método convierte la ecuación diferencial en un sistema de ecuaciones lineales que se puede resolver con técnicas de álgebra. Básicamente, se aproximan las derivadas de la función usando los valores de la función en puntos cercanos.
Por ejemplo, la segunda derivada de una función se puede aproximar con la fórmula:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{u_{i+1}- 2 u_i + u_{i-1}}{h^2}
Donde 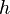 es la distancia entre los puntos. Al aplicar estas aproximaciones a la ecuación diferencial en muchos puntos, se crea un sistema de ecuaciones que se puede resolver para encontrar la solución aproximada.
es la distancia entre los puntos. Al aplicar estas aproximaciones a la ecuación diferencial en muchos puntos, se crea un sistema de ecuaciones que se puede resolver para encontrar la solución aproximada.
Galería de imágenes
Véase también
 En inglés: Numerical methods for ordinary differential equations Facts for Kids
En inglés: Numerical methods for ordinary differential equations Facts for Kids


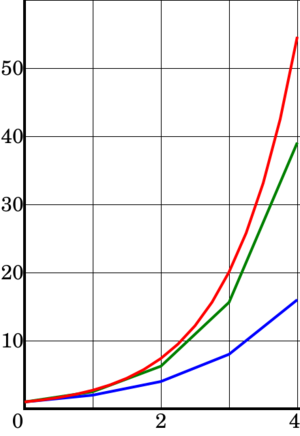
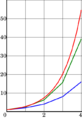
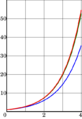
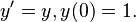 Azul: el Método de Euler, verde: el método del punto medio, rojo: la solución exacta,
Azul: el Método de Euler, verde: el método del punto medio, rojo: la solución exacta, 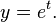 El tamaño del paso es
El tamaño del paso es 
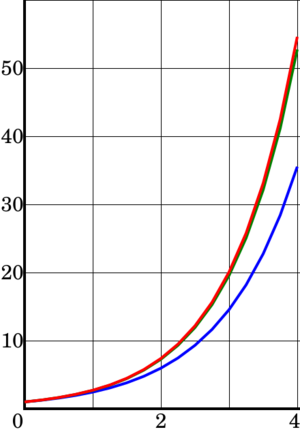
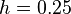 . Se ve que el método del punto medio converge más rápido que el método de Euler
. Se ve que el método del punto medio converge más rápido que el método de Euler