Error estándar para niños
El error estándar es una medida que nos ayuda a entender qué tan precisa es una estimación que hacemos a partir de una muestra de datos. Imagina que quieres saber la estatura promedio de todos los estudiantes de tu escuela. No puedes medir a todos, así que mides a un grupo (una muestra). El promedio de ese grupo será una estimación. El error estándar nos dice qué tan cerca es probable que esté ese promedio de muestra del promedio real de todos los estudiantes.
Es como si tomaras varias muestras diferentes de la misma población; cada muestra te daría un promedio ligeramente distinto. El error estándar es la desviación estándar de todos esos promedios de muestra. Cuanto más pequeño sea el error estándar, más confianza podemos tener en que el promedio de nuestra muestra está cerca del promedio real de toda la población.
Contenido
¿Qué es el error estándar de la media?
Cuando calculamos el promedio de una muestra (la media muestral), queremos que sea una buena representación del promedio de toda la población. Sin embargo, si tomamos diferentes muestras de la misma población, es muy probable que obtengamos promedios ligeramente distintos.
El error estándar de la media nos dice cuánto se espera que varíen esos promedios de muestra. Es la desviación estándar de todos los posibles promedios que podríamos obtener de muestras del mismo tamaño tomadas de una población. En otras palabras, nos indica qué tan dispersos están los promedios de las muestras alrededor del promedio real de la población.
En la práctica, el valor exacto de la desviación estándar de toda la población casi nunca se conoce. Por eso, el término "error estándar" a menudo se refiere a una estimación de esta cantidad desconocida, calculada a partir de los datos de nuestra muestra.
Cálculo del error estándar de la media
Para entender cómo se calcula el error estándar de la media, necesitamos conocer dos cosas: la desviación estándar de la población y el tamaño de nuestra muestra.
Valor exacto (si conocemos la población)
Si tuviéramos la suerte de conocer la desviación estándar (que se representa con la letra griega sigma, σ) de toda la población, el error estándar de la media (σx̄) se calcularía así:
- σx̄ = σ / √n
Donde:
- σ es la desviación estándar de la población.
- n es el tamaño de la muestra (el número de observaciones o datos que tenemos).
Esta fórmula nos muestra algo importante: cuanto más grande sea nuestra muestra (mayor n), más pequeño será el error estándar. Esto significa que una muestra más grande nos da una estimación más precisa del promedio de la población. Por ejemplo, para reducir el error a la mitad, necesitaríamos una muestra cuatro veces más grande.
Estimación (lo más común)
Como casi nunca conocemos la desviación estándar real de la población (σ), la estimamos usando la desviación estándar de nuestra propia muestra (que se representa con la letra s). Así, la fórmula para estimar el error estándar de la media es:
- σx̄ ≈ s / √n
Donde:
- s es la desviación estándar de la muestra.
- n es el tamaño de la muestra.
Es importante saber que, si la muestra es muy pequeña, esta estimación del error estándar puede ser un poco menor de lo que realmente es. Sin embargo, a medida que el tamaño de la muestra aumenta, esta estimación se vuelve muy precisa.
Usos del error estándar
El error estándar es muy útil en estadística porque nos ayuda a entender la incertidumbre de nuestras mediciones.
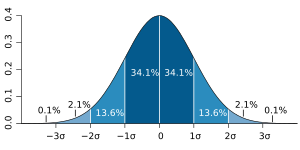
- Intervalos de confianza: Una de sus aplicaciones más comunes es para crear "intervalos de confianza". Estos intervalos nos dan un rango de valores donde es muy probable que se encuentre el verdadero promedio de la población. Por ejemplo, un intervalo de confianza del 95% significa que estamos 95% seguros de que el promedio real de la población está dentro de ese rango.
Para calcular un intervalo de confianza aproximado del 95% para la media, se usan estas fórmulas: * Límite superior del 95% = promedio de la muestra + (error estándar × 1.96) * Límite inferior del 95% = promedio de la muestra - (error estándar × 1.96)
El número 1.96 viene de la distribución normal y se usa comúnmente para intervalos del 95%.
- Comparación de datos: También se usa para comparar diferentes grupos de datos o para evaluar la precisión de modelos estadísticos, como en el análisis de regresión.
Error estándar de la media vs. Desviación estándar
Es fácil confundir el error estándar de la media con la desviación estándar, pero son diferentes:
- La desviación estándar de una muestra nos dice cuánto varían los datos individuales dentro de esa muestra con respecto a su propio promedio. Es una medida de la dispersión de los datos.
- El error estándar de la media nos dice qué tan lejos es probable que esté el promedio de nuestra muestra del promedio real de toda la población. Es una medida de la precisión de nuestra estimación del promedio de la población.
En resumen, la desviación estándar describe la variación dentro de una muestra, mientras que el error estándar de la media describe la variación entre los promedios de diferentes muestras. A medida que el tamaño de la muestra aumenta, el error estándar de la media se hace más pequeño (porque nuestra estimación del promedio de la población es más precisa), mientras que la desviación estándar de la muestra tiende a parecerse más a la desviación estándar de la población.
Galería de imágenes
-
Para un valor dado en una muestra aleatoria con un error distribuido normal, la imagen de arriba representa la proporción de muestras que pueden caer entre 0,1,2, y 3 desviaciones estándar por encima y por debajo del valor real.
Véase también
En inglés: Standard error Facts for Kids
