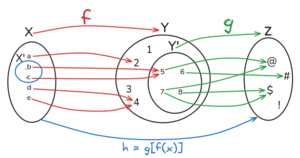
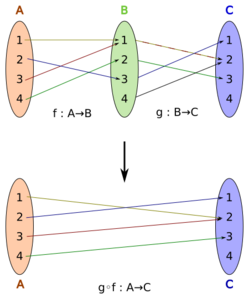
Función compuesta para niños

Una función compuesta es como una cadena de máquinas matemáticas. Imagina que tienes dos máquinas: una que toma un número y hace algo con él, y otra que toma el resultado de la primera y hace algo más. La función compuesta es el resultado de usar esas dos máquinas una después de la otra.

En matemáticas, esto significa que aplicamos una función a un número, y luego aplicamos otra función al resultado que obtuvimos.

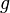Usamos un símbolo especial para esto: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): g \circ f . Se lee "g compuesta con f". Esto significa que primero aplicas la función y luego aplicas la función al resultado.

Por ejemplo, si tienes un número x, primero calculas . Luego, tomas ese resultado y lo usas como entrada para la función 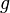, obteniendo Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): g(f(x)) .

¿Qué es una función compuesta?

Una función compuesta se forma cuando el resultado de una función se convierte en la entrada de otra función. Es como un proceso de dos pasos.

Cómo se define una función compuesta

Para que puedas combinar dos funciones, el "territorio de salida" (la imagen) de la primera función debe coincidir con el "territorio de entrada" (el dominio) de la segunda función.

Por ejemplo, si tienes:

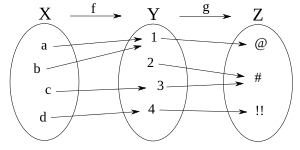
• Una función que va de un conjunto X a un conjunto Y.
• Y otra función 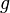que va del conjunto Y a un conjunto Z.

Entonces, la función compuesta Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (g \circ f) va directamente del conjunto X al conjunto Z.

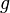Esto significa que para cada elemento x en X, primero calculas (que te da un valor en Y). Luego, usas ese valor como entrada para , obteniendo Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): g(f(x)) (que te da un valor en Z).

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): g \circ f es la función que resulta de aplicar primero y luego 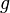. En el ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (g \circ f) (a)= @

El dominio de la composición Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): g \circ f está formado por los elementos del dominio de para los que pertenece al dominio de .

Propiedades importantes

Las funciones compuestas tienen algunas propiedades interesantes:

La composición es asociativa

Esto significa que si tienes tres funciones, por ejemplo, , 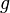y 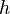, no importa cómo las agrupes al componerlas. El resultado será el mismo: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f \circ (g \circ h) = (f \circ g) \circ h Esto es útil porque nos permite escribir Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f \circ g \circ h sin preocuparnos por los paréntesis.

La composición no es conmutativa

A diferencia de la suma o la multiplicación de números, el orden en que compones las funciones sí importa. Casi siempre, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (g \circ f) es diferente de Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (f \circ g) .

Por ejemplo:

• Si Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(x) = x+1 (sumar 1)
• Y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): g(x) = x^2 (elevar al cuadrado)

Entonces:

• Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (f \circ g)(x) = f(g(x)) = f(x^2) = x^2+1 (primero elevas al cuadrado, luego sumas 1)
• Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (g \circ f)(x) = g(f(x)) = g(x+1) = (x+1)^2 = x^2+2x+1 (primero sumas 1, luego elevas al cuadrado)

Como puedes ver, los resultados son diferentes.

Las composiciones de dos funciones, el valor absoluto y una función cúbica, en distintos órdenes, muestran que la composición no es conmutativa.

La función identidad

Existe una función especial llamada función identidad, que no cambia nada. Si la compones con cualquier otra función, el resultado es la función original. Es como multiplicar por 1.

Inversa de una composición

Si tienes una función compuesta Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (g \circ f) y quieres encontrar su función inversa, el orden de las inversas se invierte: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (g \circ f)^{-1} = f^{-1} \circ g^{-1} Esto significa que para "deshacer" Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): g \circ f , primero "deshaces" 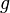y luego "deshaces" .

Ejemplos de funciones compuestas

Aquí tienes algunos ejemplos para entender mejor:

• Ejemplo con números:

* Si Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(x) = 2x + 4 (multiplicar por 2 y sumar 4) * Y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): g(x) = x^3 (elevar al cubo)

Entonces: * Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (f \circ g)(x) = f(g(x)) = f(x^3) = 2(x^3) + 4 * Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (g \circ f)(x) = g(f(x)) = g(2x + 4) = (2x + 4)^3

• Ejemplo con un avión:

* Imagina que Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a(t) es la altitud de un avión en un momento t. * Y 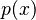es la presión atmosférica a una altitud x.

Entonces, la función compuesta Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (p \circ a)(t) te daría la presión alrededor del avión en el momento t. Primero calculas la altitud del avión en ese momento, y luego usas esa altitud para encontrar la presión.

Ejemplo concreto de composición de dos funciones.

Potencias funcionales

Cuando una función se compone consigo misma varias veces, lo llamamos potencia funcional o función iterada.

• Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f^2(x) = (f \circ f)(x) = f(f(x)) (aplicar f dos veces)
• Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f^3(x) = (f \circ f \circ f)(x) = f(f(f(x))) (aplicar f tres veces)

Y así sucesivamente. Por convención, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f^0(x) se define como la función identidad, que simplemente devuelve x.

¿Por qué una función compuesta está "bien definida"?

Una función compuesta está "bien definida" porque cumple con dos condiciones importantes:

1. Existe: Para cada valor de entrada x, siempre podemos encontrar un resultado único. Primero, nos da un valor. Luego, 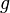toma ese valor y nos da un resultado final. 2. Es única: Como y 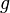son funciones que siempre dan un único resultado para cada entrada, la función compuesta Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): g(f(x)) también dará un único resultado para cada x.

Véase también

En inglés: Function composition Facts for Kids