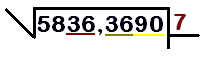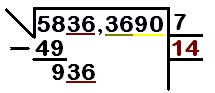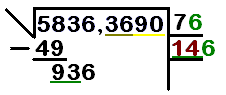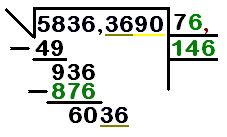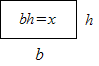Cálculo de la raíz cuadrada para niños
Calcular la raíz cuadrada de un número real positivo es como encontrar un número que, al multiplicarse por sí mismo, te dé el número original. Por ejemplo, la raíz cuadrada de 25 es 5, porque 5 multiplicado por 5 es 25. Existen diferentes maneras de encontrar la raíz cuadrada de un número, desde métodos manuales hasta algoritmos que usan las computadoras.
Cómo Calcular la Raíz Cuadrada
Para calcular la raíz cuadrada de un número, buscamos ese valor especial que, al multiplicarse por sí mismo, nos devuelve el número inicial. Es una operación muy útil en matemáticas y en la vida diaria.
El Método Paso a Paso (Dígito a Dígito)
Este es un método manual para calcular la raíz cuadrada, muy parecido a la división. Es útil para entender cómo funciona la raíz cuadrada.
Partes de la Raíz Cuadrada
Para entender este método, es importante conocer sus partes:
- Radical: Es el símbolo especial que nos dice que estamos calculando una raíz cuadrada (parece una "v" con una línea encima).
- Radicando: Es el número al que le vamos a calcular la raíz cuadrada. Se encuentra dentro del radical.
- Renglón de la raíz cuadrada: Aquí escribiremos el resultado de nuestra raíz cuadrada.
- Renglones auxiliares: Son líneas donde hacemos cálculos intermedios para ayudarnos a resolver.
- Residuo: Es lo que sobra al final de la operación, si la raíz cuadrada no es exacta.
Pasos para Calcular la Raíz Cuadrada
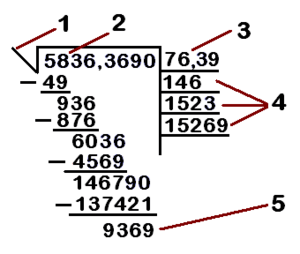
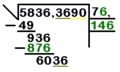
Vamos a usar el número 5836,3690 como ejemplo para seguir los pasos:
- Paso 1: Separar en grupos de dos cifras.
* Desde el punto decimal, separa el número en grupos de dos cifras hacia la izquierda y hacia la derecha. * Si no hay decimales, empieza desde la derecha. * Si al final de los decimales queda una cifra sola, añade un cero para completar el grupo. * En nuestro ejemplo (5836,3690), separamos así: 58 / 36 , 36 / 90.
- Paso 2: Encontrar el primer número de la raíz.
* Busca un número que, multiplicado por sí mismo (al cuadrado), sea igual o lo más cercano posible al primer grupo de la izquierda (en nuestro caso, 58), pero sin pasarse. * Para 58, el número es 7, porque 7 x 7 = 49. Si fuera 8 x 8 = 64, se pasaría. * Escribe el 7 en el renglón de la raíz.
- Paso 3: Restar y bajar el siguiente grupo.
* Multiplica el número que encontraste (7) por sí mismo (7 x 7 = 49). * Resta 49 de 58 (58 - 49 = 9). * Baja el siguiente grupo de dos cifras (36) junto al resultado de la resta. Ahora tienes 936. * En el renglón auxiliar, multiplica el número de la raíz (7) por 2 (7 x 2 = 14).
- Paso 4: Encontrar el siguiente número de la raíz.
* Ahora, busca un número n que, al añadirlo al 14 (formando 14n) y multiplicarlo por ese mismo n, te dé un resultado igual o menor a 936. * Por ejemplo, 141 x 1, 142 x 2, etc. * Una forma de estimar es dividir las primeras cifras de 936 (93) entre 14. El resultado (6 y algo) nos da una pista. * Probamos con 6: 146 x 6 = 876. Este es el más cercano sin pasarse. * Escribe el 6 en el renglón de la raíz, al lado del 7. Ahora la raíz es 76.
- Paso 5: Restar y bajar el siguiente grupo (con decimales).
* Resta 876 de 936 (936 - 876 = 60). * Baja el siguiente grupo de cifras (36). Ahora tienes 6036. * Como este grupo (36) está después del punto decimal en el radicando original, debes poner un punto decimal en el renglón de la raíz (después del 76).
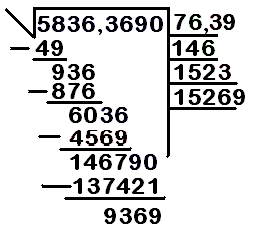
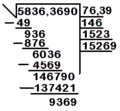
- Paso 6: Continuar el proceso.
* Multiplica el número actual de la raíz (76, ignorando el decimal por ahora) por 2 (76 x 2 = 152). Escribe 152 en el renglón auxiliar. * Busca un número n que, al añadirlo a 152 (formando 152n) y multiplicarlo por n, te dé un resultado igual o menor a 6036. * Divide las primeras cifras de 6036 (603) entre 152. El resultado es aproximadamente 3. * Probamos con 3: 1523 x 3 = 4569. * Escribe el 3 en el renglón de la raíz. Ahora la raíz es 76,3. * Resta 4569 de 6036 (6036 - 4569 = 1467).
- Paso 7: Último paso del ejemplo.
* Multiplica el número actual de la raíz (763, ignorando el decimal) por 2 (763 x 2 = 1526). Escribe 1526 en el renglón auxiliar. * Baja el último grupo de cifras (90). Ahora tienes 146790. * Busca un número n que, al añadirlo a 1526 (formando 1526n) y multiplicarlo por n, te dé un resultado igual o menor a 146790. * Divide las primeras cifras de 146790 (14679) entre 1526. El resultado es aproximadamente 9. * Probamos con 9: 15269 x 9 = 137421. * Escribe el 9 en el renglón de la raíz. Ahora la raíz es 76,39. * Resta 137421 de 146790 (146790 - 137421 = 9369).
La raíz cuadrada de 5836,3690 es aproximadamente 76,39, con un residuo de 0,9369. Puedes seguir añadiendo ceros y grupos de dos para obtener más decimales.
Resumen de los Ciclos
Los pasos se repiten en ciclos:
- 1) Hallar la siguiente cifra de la raíz.
- 2) Realizar la resta.
- 3) Bajar el siguiente par de cifras del radicando.
- 4) Multiplicar la parte de la raíz que ya tienes por dos.
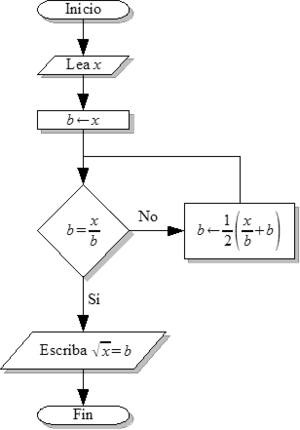
El Algoritmo Babilónico
El algoritmo babilónico es un método muy antiguo y eficiente para calcular raíces cuadradas. Se basa en la idea de que si tienes un rectángulo con un área igual al número al que le buscas la raíz, puedes ir ajustando sus lados hasta que se parezca mucho a un cuadrado. Cuando el rectángulo es casi un cuadrado, la longitud de sus lados es una buena aproximación de la raíz cuadrada.
Cómo Funciona el Algoritmo Babilónico
Imagina que quieres encontrar la raíz cuadrada de un número, por ejemplo, 25. 1. Empieza con una suposición: Elige un número que creas que podría ser la raíz cuadrada. No tiene que ser perfecto. Por ejemplo, para 25, podrías empezar con 4. 2. Calcula el otro lado: Divide el número original (25) entre tu suposición (4). Esto te da el "otro lado" del rectángulo (25 / 4 = 6.25). 3. Encuentra el promedio: Calcula el promedio de tu suposición (4) y el "otro lado" (6.25). (4 + 6.25) / 2 = 5.125. Este nuevo número es una mejor suposición. 4. Repite: Usa este nuevo promedio (5.125) como tu nueva suposición y repite los pasos 2 y 3. * 25 / 5.125 = 4.878 * (5.125 + 4.878) / 2 = 5.0015 5. Sigue repitiendo: Cuantas más veces repitas estos pasos, más cerca estarás de la raíz cuadrada real. Verás que las suposiciones se acercan cada vez más a 5.
Este método es muy poderoso porque converge rápidamente, es decir, te da una respuesta muy precisa en pocas repeticiones.
Aproximación de Bakhshali
Este es otro método antiguo para encontrar una buena aproximación de la raíz cuadrada. Fue descrito en un manuscrito llamado manuscrito de Bakhshali. Es como una versión mejorada del método babilónico.
Ejemplo con la raíz cuadrada de 10,5
Si queremos calcular la raíz cuadrada de 10,5 con este método: 1. Primero, buscamos el número entero cuyo cuadrado esté más cerca de 10,5. Ese número es 3, porque 3 al cuadrado es 9 (que está más cerca de 10,5 que 4 al cuadrado, que es 16). Así que, nuestro número de partida es 3. 2. Luego, usamos una fórmula especial: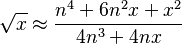 
Donde 'x' es el número al que le buscamos la raíz (10,5) y 'n' es nuestro número de partida (3). 3. Sustituimos los valores en la fórmula: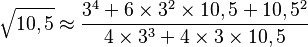 
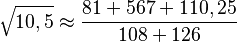
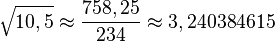Este método nos da una aproximación bastante buena de la raíz cuadrada.
Galería de imágenes
-
Paso 1.
-
Paso 2.
-
Paso 3.
-
Paso 4.
-
Paso 5.
-
Paso 6.
-
Paso 7.
Véase también
