Archivo: Surface integral - definition

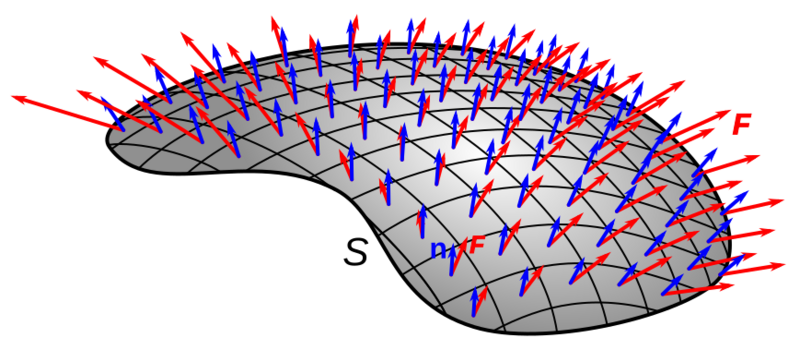
Descripción: Diagram illustrating how a surface integral of a vector field over a surface is defined. It shows an arbitrary surface S with a vector field F, (red arrows) passing through it. The surface is divided into small (infinitesimal) regions dS. The surface integral is the sum of the perpendicular component of the field passing through each region multiplied by the area dS. The perpendicular component of the field is equal to the dot product of the field F(x) with the unit normal vector n(x) at the point dS: ∫ S F ⋅ n d S {\displaystyle \int _{S}{\mathbf {F\cdot n}}dS}
Título: Surface integral - definition
Créditos: Trabajo propio
Autor(a): Chetvorno
Términos de Uso: Creative Commons Zero, Public Domain Dedication
Licencia: CC0
Enlace de Licencia: http://creativecommons.org/publicdomain/zero/1.0/deed.en
¿Se exige la atribución?: No