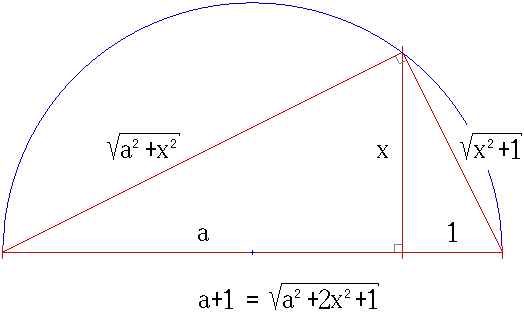Archivo: SqrtGeom

Descripción: Straightedge and compass construction of the length x = a {\displaystyle x={\sqrt {a}}} , given the length a {\displaystyle a} and the unit length. The proof relies on Thales's theorem (blue circle) to obtain a right triangle with hypothenuse length a + 1 {\displaystyle a+1} , and on the Pythagorean theorem to set up equations about its height and side lengths, viz. a 2 + x 2 = a 2 + x 2 2 {\displaystyle a^{2}+x^{2}={\sqrt {a^{2}+x^{2}}}^{2}} (from the left triangle; trivially satisfied), 1 2 + x 2 = x 2 + 1 2 {\displaystyle 1^{2}+x^{2}={\sqrt {x^{2}+1}}^{2}} (from the right triangle; trivially satisfied), and a 2 + x 2 2 + x 2 + 1 2 = ( a + 1 ) 2 {\displaystyle {\sqrt {a^{2}+x^{2}}}^{2}+{\sqrt {x^{2}+1}}^{2}=(a+1)^{2}} (from the big triangle). Their unique positive solution is x = a {\displaystyle x={\sqrt {a}}} .
Título: SqrtGeom
Créditos: Trabajo propio, inspired from File:TomoyukiMogi(SquareRoot).gif.
Autor(a): Jochen Burghardt
Términos de Uso: Creative Commons Attribution-Share Alike 4.0
Licencia: CC BY-SA 4.0
Enlace de Licencia: https://creativecommons.org/licenses/by-sa/4.0
¿Se exige la atribución?: Sí