Archivo: Mplwp universe scale evolution

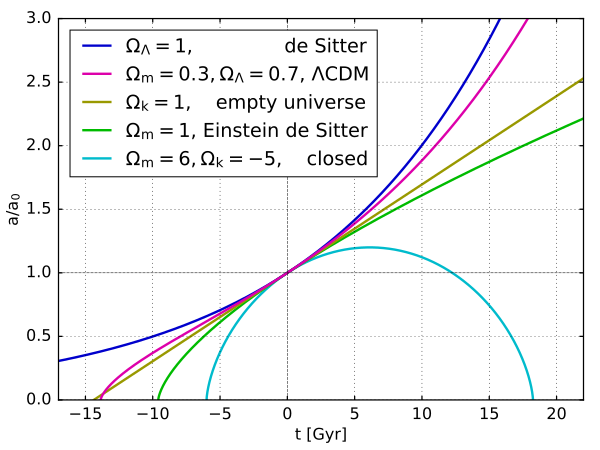
Descripción: Plot of the evolution of the size of the universe (scale parameter a) over time (in billion years, Gyr). Different models are shown, which are all solutions to the Friedmann equations with different parameters. The evolution is governed by the equation ( a ˙ a ) 2 = H 0 2 ( Ω r a 4 + Ω m a 3 + Ω k a 2 + Ω Λ ) {\displaystyle \left({\frac {\dot {a}}{a}}\right)^{2}=H_{0}^{2}\left({\frac {\Omega _{r}}{a^{4}}}+{\frac {\Omega _{m}}{a^{3}}}+{\frac {\Omega _{k}}{a^{2}}}+\Omega _{\Lambda }\right)} . Here Ω r {\displaystyle \Omega _{r}} is the radiation density, Ω m {\displaystyle \Omega _{m}} the matter density, Ω k {\displaystyle \Omega _{k}} the curvature parameter and Ω Λ {\displaystyle \Omega _{\Lambda }} the dark energy, all normalized such that Ω r + Ω m + Ω k + Ω Λ = 1 {\displaystyle \Omega _{r}+\Omega _{m}+\Omega _{k}+\Omega _{\Lambda }=1} represents the fact that today's expansion rate is H 0 {\displaystyle H_{0}} . Plotted parameter sets: De Sitter universe: Only dark energy: Ω Λ = 1 {\displaystyle \Omega _{\Lambda }=1} Lambda-CDM model: The model that fits the observations best: Ω m = 0.3 {\displaystyle \Omega _{m}=0.3} , Ω Λ = 0.7 {\displaystyle \Omega _{\Lambda }=0.7} An empty universe (no relevant contributions of matter, radiation, dark energy) with negative curvature: Ω k = 1 {\displaystyle \Omega _{k}=1} Einstein–de_Sitter universe: A flat universe dominated by cold matter: Ω m = 1 {\displaystyle \Omega _{m}=1} A closed Friedmann model: Ω m = 6 {\displaystyle \Omega _{m}=6} , Ω k = − 5 {\displaystyle \Omega _{k}=-5}
Título: Mplwp universe scale evolution
Créditos: Trabajo propio
Autor(a): Geek3
Términos de Uso: Creative Commons Attribution-Share Alike 4.0
Licencia: CC BY-SA 4.0
Enlace de Licencia: https://creativecommons.org/licenses/by-sa/4.0
¿Se exige la atribución?: Sí