Archivo: Abu Reyhan Biruni-Earth Circumference

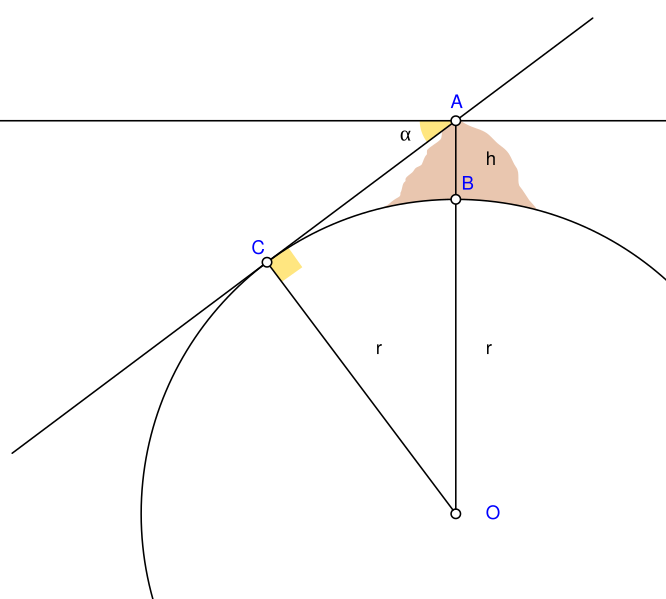
Descripción: Biruni (973 - 1048) developed a new method using trigonometric calculations to compute earth's radius and circumference based on the angle between the horizontal line and true horizon from a mountain top with known height. He calculated the height of the mountain by going to two points at sea level with a known distance apart and then measuring the angle between the plain and the top of the mountain for both points. Biruni's estimate of 6,339.9 km for the Earth radius had an error of 0.0026 and was 16.8 km less than the current value of 6,356.7 km. The idea came to him when he was on top of a tall mountain near Nandana in Pakistan. He measured the dip angle using an astrolabe and he applied to the law of sines formula. He also made use of algebra in his calculation. A = Highest point of mountain B = Lowest point of mountain h = Height of the mountain C = Lowest point of true horizon visible from point A O = Centre of Earth α = Dip angle r = Earth's radius Solution: The angle AOC = α. AO=(r+h) is the hypotenuse in triangle AOC. r=(r+h)·cos(α) Then the right side can be simplified to find r. r=h·cos(α)/(1-cos(α))
Título: Abu Reyhan Biruni-Earth Circumference
Créditos: Trabajo propio Using Geogebra and Inkscape
Autor(a): Nevit Dilmen
Términos de Uso: Creative Commons Attribution-Share Alike 3.0
Licencia: CC BY-SA 3.0
Enlace de Licencia: https://creativecommons.org/licenses/by-sa/3.0
¿Se exige la atribución?: Sí